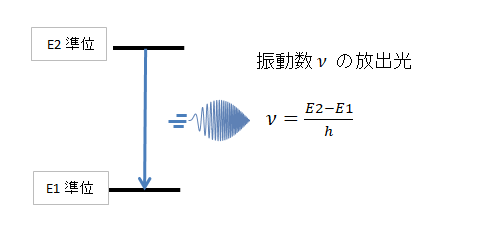
光の発生機構の一つとしてエネルギー準位差に応じた振動数の光を放出します(図3)。これは原子に特有の離散した振動数の光(スペクトル線)を出します。これ以外に重要なものとして入射光電粒子に原子が共鳴して光源と作用点の相対速度が0であれば、同じ振動数の光を再放出する機構があります(図4)。この場合スペクトル線のように離散したものでなく入射光が広い周波数帯域を持っていれば放出光も同じ範囲の振動数で連続的なスペクトルになります。

図3 エネルギー準位差による発光
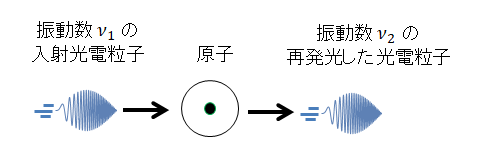
図4 共鳴による再発光
電磁波も光も振動数が異なるだけで同じものです。光電粒子理論ではそれらは粒子なので電磁気の物理法則は
① 1個の粒子が持つエネルギー と
② 粒子の数
の集合体として記述されます。1個の粒子に内在する波動により波としての性質も持ちます。電磁波と光が示す波動的な性質もその中で説明されます。
マクスウエル電磁気理論では B = rot A として表されるベクトルポテンシャル A が用いられています。A は数学的には値が定まらない不確かさを持っていますが物理的な実態があるものとして考えられています。磁束密度 B だけでは問題が解けない電磁場の問題も A を用いることで解決します。例えば密に巻いたソレノイドコイルの外側の磁束密度 B は 0 になるので B からは電磁誘導による E を求めることができません
( rot E = - ∂B /∂t から E は 0 になる)。
しかし物理的な実態として存在するベクトルポテンシャル A はソレノイドコイル外側で 0 ではないのでこれにより E を求めることができます ( E = - ∂A /∂t )。 次にソレノイドコイル中心部でのローレンツ力を求めることを想定します。中心部では A が 0 になりますが B は 0 でありません。今度は逆にA でなく、 B を用いてローレンツ力を求めることになります。
このようにベクトルポテンシャル A は部分的に有用ですがそれだけでは解を求めることができません。
これに対して光電粒子理論では A は数学的な利便性から使うことはあっても物理的に何か存在しているものとして位置付けてはいません。ソレノイドコイルの電磁誘導現象も A ではなく粒子の飛来衝突によりすべて説明されます。
どのようにして理論を構築するのかということになりますが、従来から用いられている電場の強さ E と磁束密度 B に速度ベクトル C0 +V が基本になります。ここで C0 は光速度定数、V は光源と作用点との相対速度です。速度ベクトルの加法は相対論的なものではなく、ガリレイ変換によります。