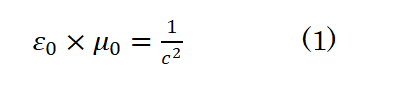
磁石の吸引力などの電磁気現象はマクスウエル理論以前は伝達速度を考慮することなく瞬時に伝わると考えられていました(遠隔作用説)。マクスウエル以後は真空中を光の速度で電磁波が伝搬するとし、物理的性質を表す「場」を考えたことにより電磁気学は大きく進歩して科学技術の発展に貢献しました。波の伝達速度が媒質の性質のみで定まり、発生源の速度には影響しないことから電磁気の作用は「場」を媒質として一定の光速度 C0 で伝わるとしました。地球の運動と媒質との相対関係の議論から特殊相対性理論が登場し、それが理論的にも整合し現実の物理世界を正しく説明できるとされています。しかし特殊相対性理論は時間が遅れ、空間が短縮するという、直ちには納得できかねる結論を導いてしまうのです。
光電粒子理論では粒子の衝突により電磁気物理現象を説明します。それは電磁気現象が「場」ではなく、光電粒子の衝突により引き起こされるので、光速度一定の制約から解放されて、時間は遅れず、空間も短縮しない全く新しい物理世界が見えてきます。
電磁波は E と B の波動が真空中の「場」を伝搬するとしてマクスウエル方程式が構成されています。これに対して光電粒子理論では「エネルギーが粒子として飛来する」と考えます。その速度はC0 ではなく C0 +V です(表1)。
表1 物理理論と考え方
| 物理理論 | 作用の仕方 | 媒質 | 伝達の速度 |
| ニュートン力学 マクスウエル以前の電磁理論 |
遠隔作用説 | 考えない | 作用の伝達は瞬時 |
| マクスウェル電磁気理論 相対性理論 |
近接作用説 | 場 | 光速度定数 C0 |
| 光電粒子理論 | 粒子の衝突 | 不要 | C0 +V |
マクスウエル方程式と相対性理論は互いの相性がよく、両理論は矛盾しません。
電磁気理論では 光速度 C と真空の誘電率 ε0 と真空の透磁率 μ0 の関係は
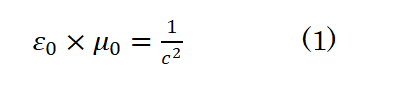
です。 ε0 と μ0 は電気力と磁気力の実験から個別に求められ、波動方程式から導かれる(1)式にそれらを代入したとき C の値が光の速度に一致しました。実験が電磁気理論の正しさを裏付けました。この限りで (1) 式の正当性には疑いありません。これを変形すれば

となります。 (2) 式には、光源や観測者の位置、速度項はありませんからそれらに関係なく光速度が定まります。真空の性質である ε0 、 μ0 は宇宙空間のどこでも変わらない定数なので、光の速さも当然空間のいたる所で一定となって特殊相対性理論の仮定 「光速度は光源、観測者の運動にかかわらず一定である」
と整合します。このようにマクスウェル方程式を「正しい」する立場では相対性理論を否定する論拠を見出すことは困難です。相対論に多くのパラドックスが提示されて疑問の主張がなされていてもいるにもかかわらずそれらは明快で理論的な根拠に欠けてしまうのです。
つまり特殊相対性理論を疑うすべての理論はマクスウエル方程式から導出される (1) 式についてそれが誤りであること、もしくは条件付きの法則 (例えば地上でしか成立しないなど)
であることを指摘しなければなりません。図1に電磁気理論から相対性理論に至る主要な法則をあげています。光電粒子理論は特殊相対性理論が誤りであるとする立場ですので、その元となるこれらの法則についてどこに誤りがあるか(誤りではないとしても適用の範囲を超えているか)を説明していきます。
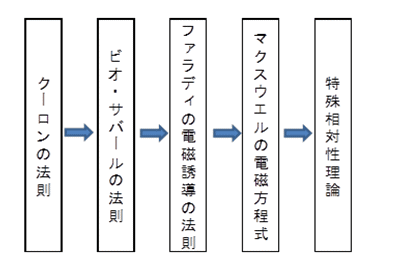
図1 電磁気理論から相対性理論に至る主要な法則
クーロンやファラディの時代では光の速度があまりに早いため一瞬で伝わるとして(遠隔作用説)電磁気現象を記述しました。その後に光と電磁波は同じものということと、光速度が有限であることが明らかになり、方程式は伝達する時間もしくは光の速度を含んだものに変更する必要がありました。どのような変更が可能でしょうか。マクスウェル方程式ではある点(作用点)の電磁気現象をその時刻よりも前に発生した発信源の遅延ポテンシャルとして記述します。遅延ポテンシャルは光の速度が一定であるという前提であれば良いのですが、光電粒子理論では光速度は一定ではありませんので代わりに、伝達の速さが変わることを前提とした速度ベクトル C0 +V を用います。ここで C0 は光速度定数、V は光源と作用点との相対速度です。クーロンの法則やファラディの電磁誘導の法則も速度ベクトル C0 +V を用いた形に変更されます。
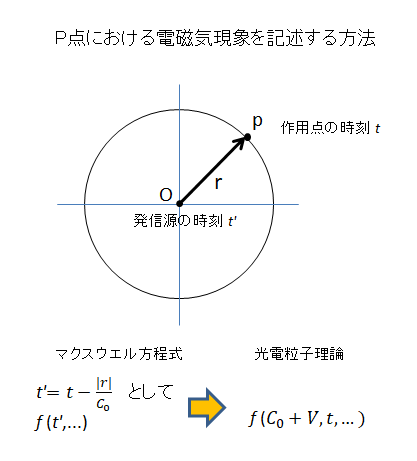
図2 遅延ポテンシャルから速度ベクトルの導入