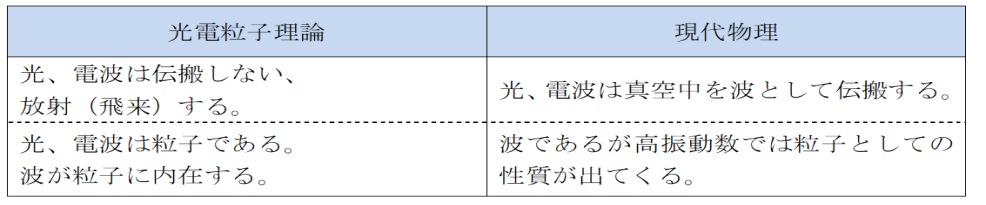
光電粒子理論の基本仮定を説明します。わかりやすいように電磁気理論・相対性理論と対比しています。
光や電波は電荷の振動により発生し、放射・飛来します。波としての振動数、波長、速度があり、粒子としての数、エネルギー、放射の向きといった性質を有します。その物理的な描像をイメージするのは日常から類推することは難しい。あえて言えば光や電波は波動の弾丸のようなものといえます。ある形をした振動エネルギーが弾丸のように飛来し物質と衝突して、原子を励起し、透過し、反射し、方向を変え、エネルギーを減じ、熱に変換されます。
光電粒子理論では粒子としての性質から当然媒質は不要です。（以下光と電波を区別して記述しません。便宜上光と書きますが電波でも同じです）
図1 光が飛来するイメージ
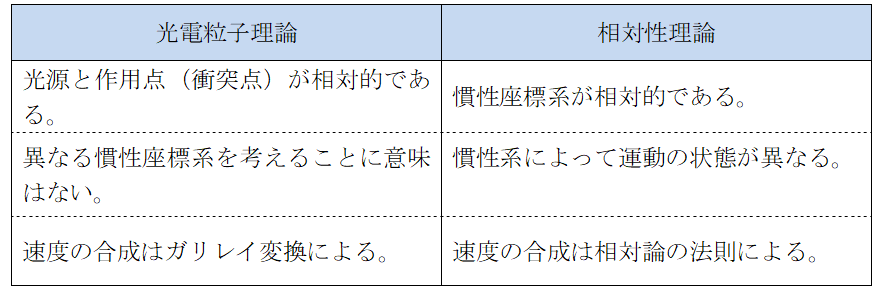
光源は光電粒子の源であり、作用点の物質に当たって物理現象を生じます。
図2において光源 S と作用点 E の距離 r において dr/dt = 0 のとき S と E の２点の位置関係は変わらず光源と作用点は互いに静止しています。
dr/dt = 定数 のときは慣性運動しています。静止と運動をこのように定義すれば、光源と作用点の２点を異なる慣性座標系からみても2点間の dr/dt の値は不変です。図3は慣性系 K で静止している光源 S を速度 V で運動する慣性系 K’にある作用点 E’から見る場合です。この場合 dr/dt = V となり、K 系で作用点が速度 V で運動していることと同じです。光源と作用点との相対関係だけが必要なことで、異なる慣性系を考えることに意味はありません。
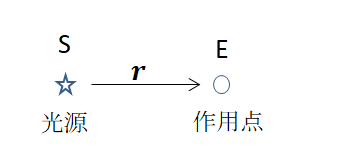
図2 光源と作用点
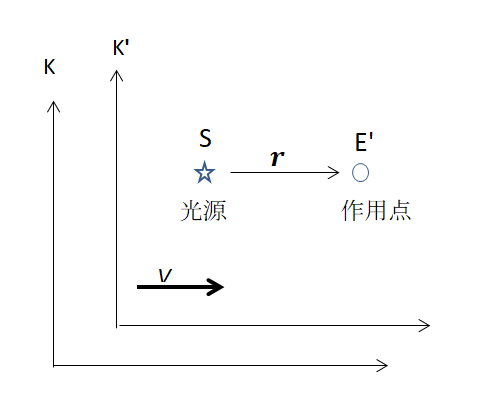
図3 慣性系 K と K'
S を恒星、E を地球として速度 V = dr/dt で運動しているとき,恒星を原点として地球が動いている（他者中心）としても、地球を原点として恒星が動いている（自分中心）としても物理法則は同じです。そもそも、どちらが静止しているか運動しているかを決めることはできません。
図4において V1 と V2 の合成速度 V はガリレイ変換にしたがいます。
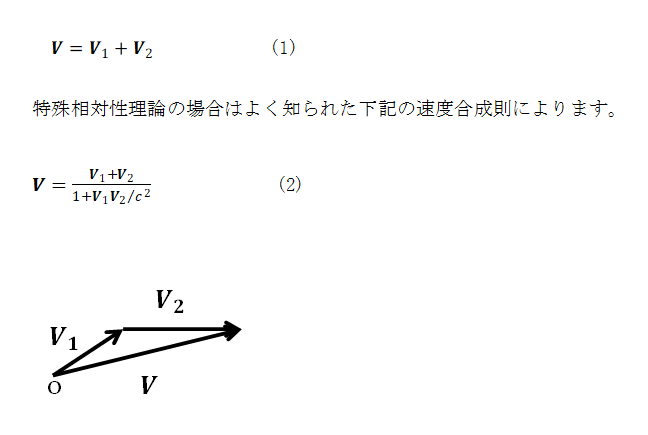
図4 合成速度ベクトル
波の一般的な性質から以下の関係があります。
ｃ = ν ×λ
すなわち 波の速度＝振動数×波長です。では速度、振動数、波長のうち、どれか1つが変化したとき、他の2つのうちどれが変化して、どれが変化しないのでしょうか。またはどれもが変化するのでしょうか。
光電粒子理論では光源（および作用点）の慣性運動では波長 λ は変わらないとします。
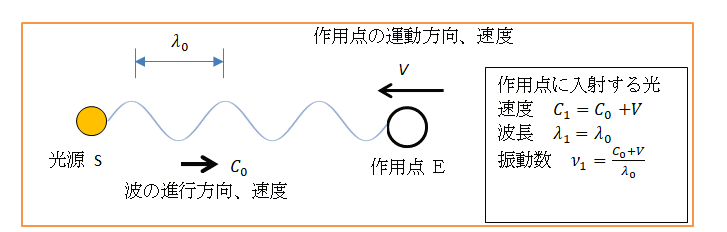
図5 光源が静止し、作用点が速度V で移動
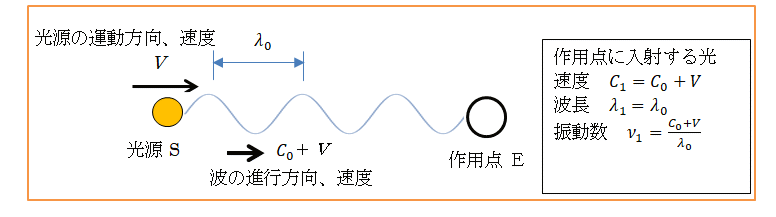
図6 作用点が静止し、光源が速度V で移動
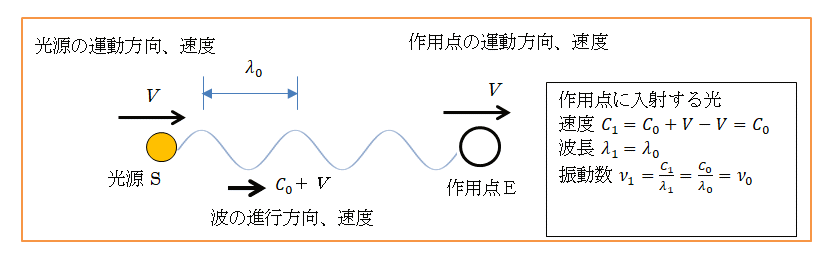
図7 光源が速度V で移動、作用点も同じ速度・方向に移動
図5では光源 S が静止、作用点 E が光源方向に速度 V で移動します。E にいる観測者は飛来する波の速度、波長、振動数を測定します。飛来する波のイメージとしては針金で作った波が飛来するとすればわかりやすい。波の相対速度は
C0 + V であり、波長 λ は変化しないので λ＝λ0 となります。
読者は今までに精密に測定された光の速度はすべて一定値 C0 であってそれ以外はないし、相対性理論による速度合成則にも合わないので波の速度を C0 + V とすることは誤りだと思われるでしょう。しかしそのことは後で説明するのでここではとりあえずそうだとしてもらいたい。振動数は相対速度と波長から ν1＝( C0＋V )/λ0 となります。図6では逆に光源 S が移動し作用点 E が静止しています。（２）運動の相対性で述べたように、S と E のどちらを運動もしくは静止としても同じなので、図5と図6のケースで違いはありません。
図7では光源と作用点が速度 V で同方向に運動している。相対速度は 0 なので全体が静止していることと同じです。
振動数は ν1＝C0/λ0＝ν0 です。
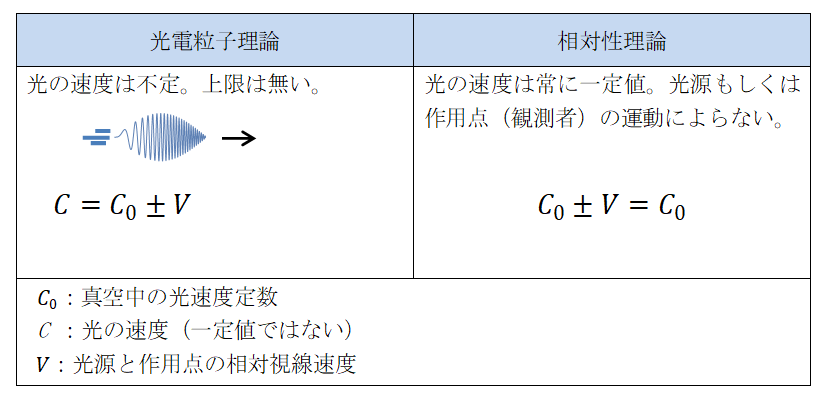
運動による変化は前述のとおりですが、これらが観測されるわけではありません。観測機器を通過することで、C は C0 に変換されるからです。このとき衝突した光は原子内の電子をその振動数で振動させて、速度 C0 の光を発生させるのです。観測される速度、振動数、波長を相対論と波動論と合わせて次の表に示します。
特殊相対性理論の場合は 
が 1 と見なせる近似で視線角度 φが 0 のときは光電粒子理論と同じになります。
表 観測される光の速度、振動数、波長
