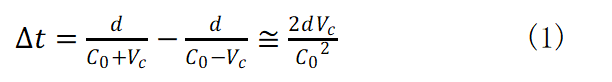
恒星の多くは二重星であり互いに公転しています。公転により地球との視線速度が変わるためもし光速度がガリレイ変換によるのであれば、みかけの公転軌道はケプラーの法則からずれることが予想されます。このことを観測したのがオランダのド・ジッターで結果は光速度が一定であることを支持するものでした。光速度は一定ではないとする光電粒子理論ではどのような説明になるでしょうか見ていきましょう。
主星の周りを伴星が周回する二重星を考えます。公転周期を P とすれば A の位置で伴星が出す光の速度は C0 +Vc 、B およびDの位置では C0 、C では C0 - Vc です。 Vc は伴星の視線速度です。位置 A と C からの光が距離 d だけ離れた地球に到達するときの時間差 Δt は
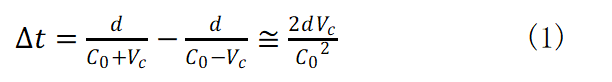
Δt が P/2 より大きいとき、A を出た光が P/2 より前にC を出た光を追い越すので地球で観測すればゴーストとして現れたり消えたりするでしょう。 Δt - P/2 <0 のときゴーストは出ません。数例の二重星で現在の観測データを用い(1)式について計算しました。右欄の「ゴースト」は Δt - P/2 <0 のとき”ゴースト無し”として、Δt - P/2 >0 のときを”ゴースト有り”として計算結果を示しています。
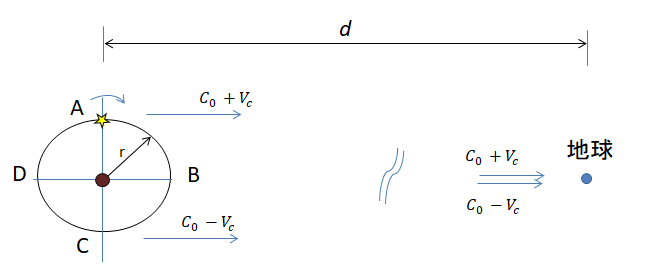
図1 二重星からの光
表1 星周塵がないときの見え方
| 区分 | 名称 | Vc | P | d | Δt - P/2 | ゴースト |
| km/s | 光年 | |||||
| 近距離可視光二重星 | おおいぬ座α星 (シリウス) |
23 | 50年 | 8.6 | <0 | 無し |
| おとめ座γ星 | 20 | 171年 | 38 | <0 | 〃 | |
| ふたご座カストル Bb | 32 | 2.9日 | 51 | >0 | 有り | |
| 遠方 X 線パルサー | ヘルクレス座 Her X-1 |
169 | 1.7日 | 19,560 | >0 | 〃 |
| ケンタウルス座 Cen X-3 |
415 | 2.1日 | 26,080 | >0 | 〃 | |
| 小マゼラン星雲 SMC X-1 |
299 | 3.9日 | 195,600 | >0 | 〃 |
光速度が C = C0 +Vc だとすれば表1の右欄でゴースト”有り”とした二重星は地球からの距離が遠く公転周期が短いことにより公転軌道が乱れてゴーストが現れるはずですが、そのようなことは観測されていません。このことが光速度は光源の運動に影響されず常に
C0 であるとする特殊相対性理論の決定的な証拠の一つとされました。表の上3行に示す星は近距離にある星で可視光での観測です。銀河系内の比較的太陽に近い恒星でも影響のあるなしを判別することができます。下の
3行に示す星は遠方のX線パルサー星で、なかでも SMC X-1 は銀河系外の小マゼラン星雲にある遠い天体です。X線パルサーは中性子星と恒星が高速で回転している連星とみられています。その回転周期は短く、遠距離なので光速度が一定でないとすればパルサーの周期は大きく乱れたものになるでしょう。しかし観測されるパルサーの周期は一定です。どういうことでしょうか。
最近になって明らかになった天体観測の知見がポイントです。恒星の周囲には恒星から噴き出した個体微粒子やガスである星周塵が発見されています。星周塵は恒星から比較的近い距離に位置し恒星の周囲を回転しているとみられています。
光電粒子理論では恒星から C0 +Vc で放射された光は星周塵に衝突し、星周塵の視線速度をほぼゼロとすれば C0 の速度の光を再放出すると考えます。星周塵は恒星から1光年以内の距離で比較的低速度で回転していてその視線速度の変化率は主星、伴星のより大幅に小さいと考えられるので視線速度の変化率をゼロか小さいとしてもおおよそ間違いではないでしょう。星周塵の中では速度は C0/n (n は媒質の屈折率)で遅くなりますが、星周塵の出口の物質が光源となり今度は速度 C0 となって地球に届くのです。これは第2章1項で望遠鏡のレンズを出た光が C0 になると説明したことと同じです。
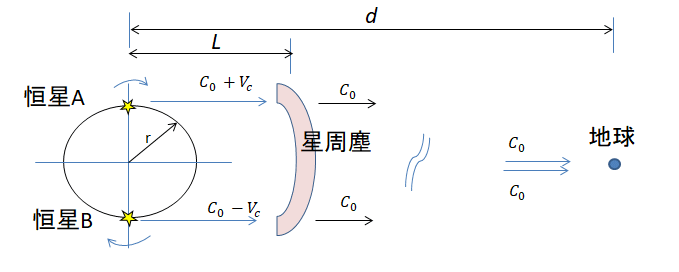
図2 二重星を取り巻く星周塵と光の速度
二重星から星周塵までの距離 L を仮におおめに見積もって 1 光年とし、(1)式 でd を L に置き換えれば、表2に示すようにいずれも Δt -P/2<0 となりゴーストは観測されないのです。
表2 星周塵があるとしたときのの見え方
| 区分 | 名称 | Vc | P | L | Δt - P/2 | ゴースト |
| km/s | 光年 | |||||
| 近距離可視光二重星 | おおいぬ座α星 (シリウス) |
23 | 50年 | 1 | <0 | 無し |
| おとめ座γ星 | 20 | 171年 | 1 | 〃 | 〃 | |
| ふたご座カストル Bb | 32 | 2.9日 | 1 | 〃 | 〃 | |
| 遠方 X 線パルサー | ヘルクレス座 Her X-1 |
169 | 1.7日 | 1 | 〃 | 〃 |
| ケンタウルス座 Cen X-3 |
415 | 2.1日 | 1 | 〃 | 〃 | |
| 小マゼラン星雲 SMC X-1 |
299 | 3.9日 | 1 | 〃 | 〃 |
コンプトン散乱は X 線が物質に衝突して波長の長い X 線を再放射する現象ですが、パルサー星からのX線が星周塵に衝突して速度 C0 の X 線を再放出することは十分に考えられることです。このように二重星からの光にゴーストがないことをもって特殊相対性理論が正しいとする根拠とはならないのです。
今までの測定実験では C0 を超える速度は見出されていません。ではどこに超光速度があるのでしょうか。地球上の光源と作用点(観測者)は相対速度が 0 なので光速度は C0です。日常の景色から出る光や放送局の電波などすべて C0 です。このように超光速度現象は地上では少ないのです。次に示すように宇宙的な現象では高エネルギー電子など、地球では接近する高速飛翔体から反射するレーダー波などが C0 を超えているとみられます。
アメリカ海洋大気庁 (NOAA )が運用する気象衛星 GOES では宇宙線の粒子数とエネルギーを計測しています。電子の飛来するエネルギーが 2 MeV を超えるものは 10 個/( cm2 s sr) 程度は普通に観測されています。電子の速度は運動エネルギー式から求められます。

ここで E:電子の運動エネルギー[J]、m:電子の質量[9.1×10-31 kg],V:電子の速度[m/s]、e:電子の電荷[1.6×10-19 J]
E の単位を eV から J に換算して計算すれば光速度定数 C0 の約2.8倍にもなります。
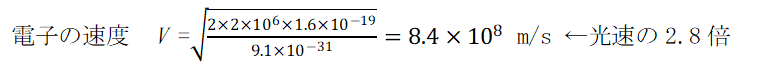
相対性理論では粒子が光速に近づくに従い質量が増加するため光速を超えることがありません。対して光電粒子理論では質量は増大しないし、光速度に制限もありません。
日本の国際宇宙ステーション「きぼう」に設置された観測装置 CALET は 1 TeV の高エネルギー電子を測定しました。この時の電子の速度は前項と同様に計算され、 C0 の約 2,000 倍にもなります。
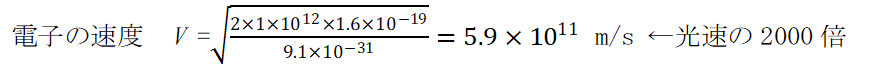
ミュー粒子は宇宙線と大気との衝突で発生し寿命は 2.2×10-6 秒 と短い。大気圏上空で発生したミュー粒子が光速度 C0 で運動しても 600 m 程度の飛行で消滅する計算ですが実際には約 15 km の厚さの大気圏を通過し地上に降り注いでいます。特殊相対性理論では光速に近い速度で飛ぶと時間がゆっくりと進むので、ミュー粒子の寿命が伸びて地上で観測できると理解されているのです。光電粒子理論では時間の進み方は一定不変であり、かつ光速度に制限はありません。ミュー粒子の速度が光速の数十倍とすれば上空で生成した粒子が地上に到達することができます。そのような光速を超えるミュー粒子はあるのでしょうか。地上で観測されているミュー粒子のエネルギーは GeV 領域です。質量は電子の 200 倍なのでミュー粒子のエネルギーを仮に 1 GeV とすればその速度は
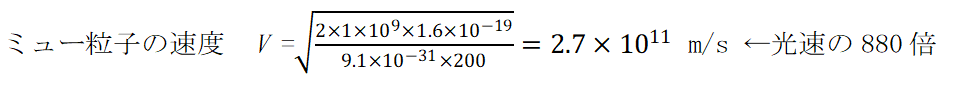
ミュー粒子が地上に到達するのに十分な速度を持っていることがわかります。
接近する高速飛翔体(航空機やロケット等)にレーダーパルスを照射してその距離を測ることを想定します。地上レーダーを原点とすれば、送信波は速度 C0 で、反射波の速度は C0 +Vc となります。相対論ではどちらも C0 です。光電粒子理論と相対論では戻ってくるレーダーパルスの時間が異なります。距離の差 Δr を試算してみました。
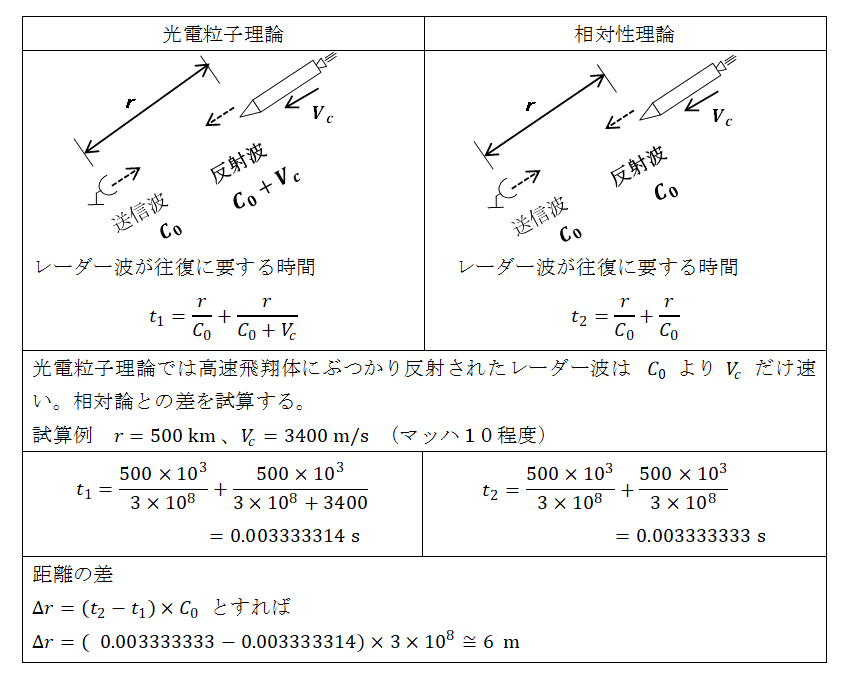
航空機は速度がマッハ1程度なのでさほど問題になりませんが、ロケットではマッハ 10~20 なので誤差も大きくなります。