
特殊相対性理論では運動する物質が光の速度(V/c=1)に近づくにつれ質量とエネルギーは急激に増大して光速と同じとき無限大になります(1式、2式および図1、図2)。

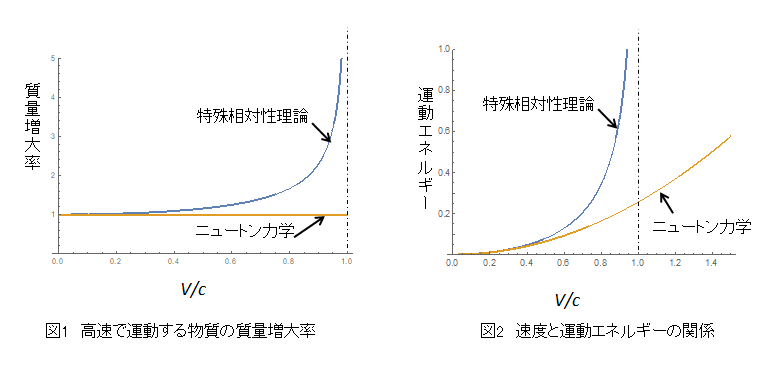
質量増大を最初に実験で検証したのは、ウォルター・カウフマン、アルフレッド・ブヘラなどです。彼らは崩壊性核種から出る高速度のベータ線を用いて磁場や電場による電子の偏向から質量の変化を測定したのです。それらの検証実験が偏向曲線や運動量などの効果を評価したうえでのいわば間接的なテストであったのに対し、ベルトッツイはMIT(マサチューセッツ工科大学)のヴァンデグラーフ発電機と線形加速器を用いて高速で運動する電子の飛行時間から速度を、熱量測定から運動エネルギーを計測する、より直接的な方法で実験を行いました。それらの実験結果は
いずれも(1)式ならびに(2)式に合致していたのです。
現在に至るまでにも多くの検証実験が繰り返されており、ベータ線を用いる方法では大学の授業でも行われています。
光電粒子理論ではニュートン力学の立場で質量は速度にかかわらず一定であるとしています。いったいどういうことでしょうか。みていきましょう。
カウフマンはラジウムなどの崩壊性核種からでるベータ線を磁場や電場により偏向させて電子の比電荷 e/m を測定しました。
均一な磁場中に入射した電子はローレンツ力による中心力が作用し円運動します(図3)。電子の速度 v 、円運動の半径 r、磁束密度B を測定することで電子の比電荷 e/m、運動量 mvが求まります。

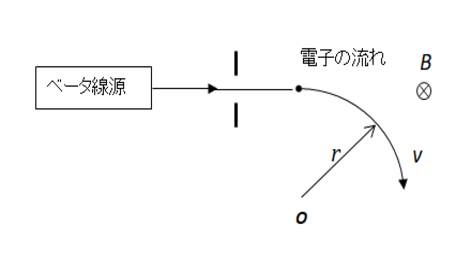
図3 電子の比電荷、運動量を測定する実験の原理図
20世紀の初頭に行われたカウフマンの実験では比電荷の減少(したがって質量又は運動量の増大)が確認されました。しかし現代のように電子の速度v,運動エネルギー K を測定する計測器がなく実験の精度をあげることが困難ななか、相対性理論のほかに別な解釈もありました。
現代では電子の速度をオシロスコープで測定でき、質量を(5)式から、運動エネルギーをシンチレーターとマルチチャンネルアナライザーによって測定できるので、(1)式および(2)式の検証が可能であり多くの実験結果はそれに合致したのでした。このような経緯があって特殊相対性理論が支持されたのです。
ベルトッツイはMITの電子加速器を用い、できるだけ直接でシンプルな方法により特殊相対性理論を検証しました。
Bertozzi, William (1964), "Speed and Kinetic Energy of Relativistic
Electrons", American Journal of Physics, 32 (7))
またありがたいことに実験の様子をYouTube でみることができます。
https://www.youtube.com/watch?v=B0BOpiMQXQA
図4にその概要を示します。
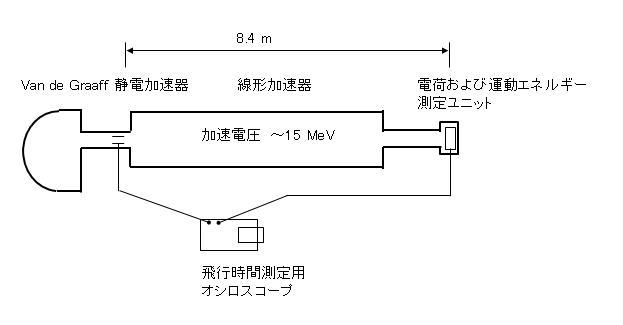
図4 ベルトッツイの実験概要図
電子を 0.5~15 MeV まで加速し、線形加速器の距離と通過する時間から電子の速度を計測しました。そして運動エネルギーを加速器終端に設けた測定ユニットの温度上昇から、電子数を検流計により測定したのです。
結果はやはり特殊相対性理論を支持するものでした。
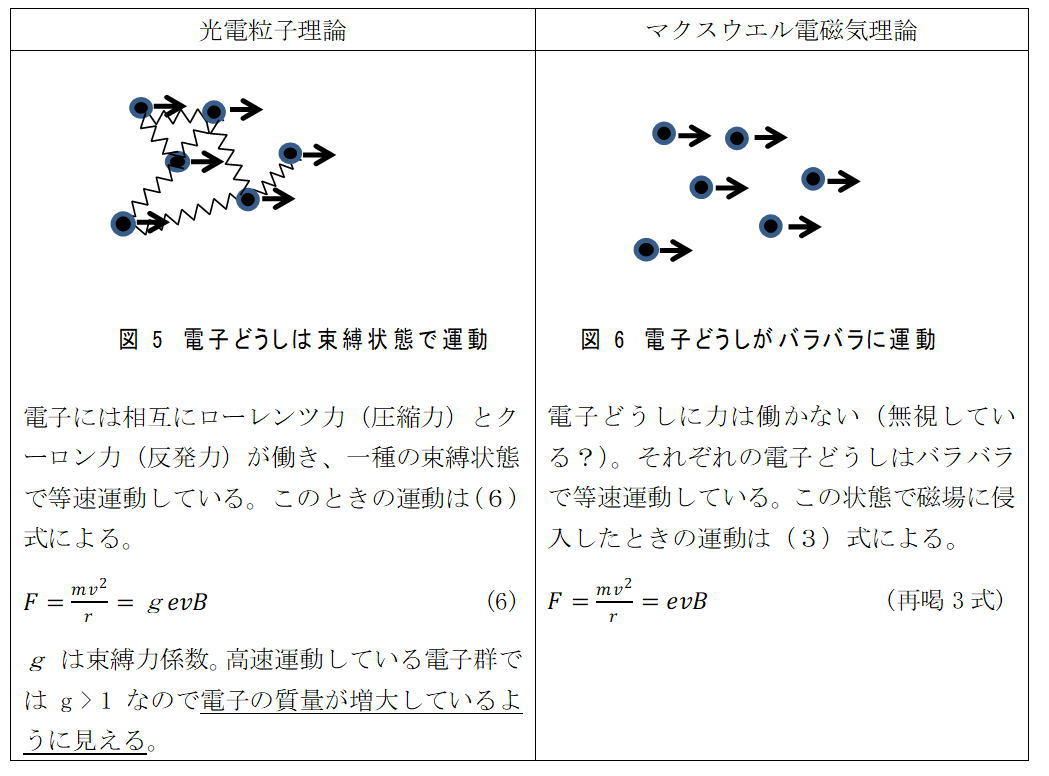
これほど特殊相対性理論を支持する実験があるなかで、それとは異なる考え方があるのでしょうか。光電粒子理論では電子群の運動法則は電子単独の運動法則とは異なると考えます。
空想の野球のボールを考えてみましょう。投手が投げるボールが仮に複数のボールであってもバラバラであれば打者がそのうちの1球を打つことは通常の打力ですみますが、ボール同士が強い束縛力があって集団でくればそれを打ち返すには大きな打力が必要です。
もしもボールを見ることができなければ(電子は見ることができないので)ボールの質量が大きくなったと感じるでしょう。
直流電流が流れている平行電線が互いに引力を及ぼすことはローレンツ力の作用として知られています。電流を i=nev とすればローレンツ力は
F= ki2/r2=k(neV)2/r2 (7)
です。この力は電線の中の電子ばかりではなく、真空中を直進する電子群にも同様に作用すると考えることは自然なことでしょう。
ここで k は比例定数、n は電子の数、V は電子の速度、r は電流間の距離。
ローレンツ力(圧縮力)は速度の2乗に比例して強くなるのに対し、クーロン力(反発力)は速度に関係しないので、電子群の速度が大きくなればローレンツ力(圧縮力)がクーロン力(反発力)を上回り、束縛力が生じます。このように
束縛力は速度の2乗に比例して強くなるのです(図7)。
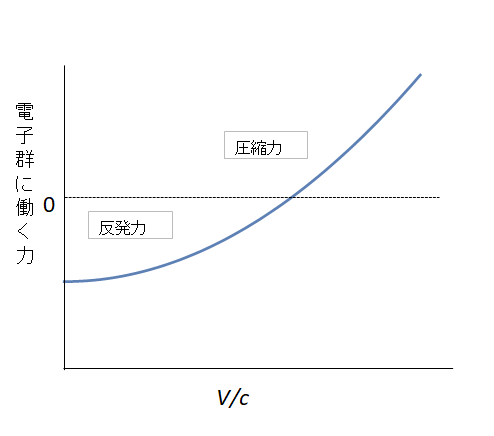
図7 電子の速度と電子群に働く力の関係
低速度で運動している電子群では弱く無視できるレベルですが光速に近いような速度では急激に大きくなり、もはや (3)式は適用できないのです。カウフマンらの実験では 適用限界を超えていたにもかかわらず(3)式を用いたことが質量は増大するとした要因になったと考えられます。
高速で直線運動する電子の速度と運動エネルギーの関係を示す(2)式は速度 V と運動エネルギー E を測定すれば検証できます。ベルトッツイは距離と飛行時間から電子の速度を、そして電子が測定ユニットのアルミディスクに衝突してその温度上昇から運動エネルギーを測定しています。
MITのヴァンデグラーフ発電機だけで1.5 MeV の加速エネルギーが得られます。このときの電子速度はニュートン力学では以下の式であらわされます。
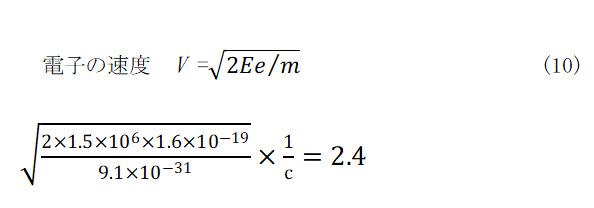
ニュートン力学では上式のように光速の約2.4倍 になるはずですが測定値は光速の0.960 倍でした。
電子群はヴァンデグラーフ発電機と直線加速器が作り出す電場によって直線的にまっすぐに飛行するのでしょうか、そうではありません。最新の電子加速器でビームの進行方向振動(シンクロトロン振動)、横方向振動(ベータトロン振動)が起こることが観測されています。つまり電子群は振動しながら進んでいるのです。
光の速度に近い速さで加速運動する電子群はローレンツ力(実際のところはローレンツ力と似た力)による束縛力(進行方向に直角な圧縮力)と進行方向とは逆向きの力(抗力)が発生します。なぜそのような力が出るのかは電磁気理論の再構築により明らかになります。
一方投入エネルギーによる推進力とクーロン反発力が生じています。これらの力により
電子群は回転もしくはジグザグ運動の振動しながら(全体としてはまっすぐに)飛行するのです。
束縛力は V2 に比例するので低速のときは無視できるレベルですが光に近い高速度では著しく大きくなります。このことにより電子の速度は大きな加速エネルギーを投じても、(10)式での計算値にはならないのです。(電子が1ケだけの加速であれば
(10)式は正しい)。
光電粒子理論では運動エネルギーは直進成分 E1と振動による成分 E2を合わせたものになります。ここでは振動は回転運動とし、放射エネルギー E3 は小さいのでここでは無視します。

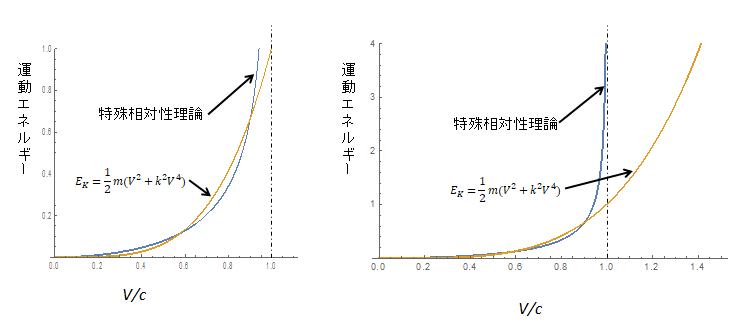
図10 v/c と運動エネルギーの関係 図11 V/c ~1.4まで表示
光速度は超えられる
(14)式の係数を適当にとり図示すれば図10に示すように特殊相対性理論の曲線とほぼ一致します。直進運動エネルギーが V の2乗に比例して増加するのに対し、振動エネルギーは V の4乗に比例して増加するので直進の速度 V を大きくするのはニュートン力学においても難しいことなのです。しかし光の速度を超えられないという制限はありません(図11)。
このようにカウフマンらの実験やベルトッツイの実験は電子群の束縛力と振動エネルギーを考慮していないことが問題だったのです。